過去の体験学習
| 年度 | 平成23年度 | ||
|---|---|---|---|
| 日付 | 平成23年8月26日 | ||
| 概要 |
『いろいろな図形を一刀両断』 永野 幸一 先生 皆さんの目の前に美味しそうなケーキがあり,無二の親友と公平に二等分することになりました.手元には一本のナイフが.こんなとき,しばしば「およそこのあたり」と見当をつけて入刀します.ケーキが円柱や直方体の形をしていると簡単です. 大学で数学を本格的に学ぶと,どんな立体図形Aも一刀両断によって(すなわち一つの平面の切り口によって),同じ体積を持つ二つの部分 A1,A2 に分割できることが分かります.では次の問題はどうでしょう.
実は分割できることが,数学の定理であるハムサンドウィッチの定理によって保証されています.つまり,A をパン,B をハム,C をパンとして,一つのハムサンドウィッチ(A,B,C) を一刀両断して,二つのハムサンドウィッチ(A1,B1,C1) と(A2,B2,C2) に二等分できるのです. 今回の体験学習では,ハムサンドウィッチの定理について学ぼうと思います.立体図形に苦手意識をお持ちの方も心配ご無用です.実習の時間には,次の二次元の問題に取り組み,実際に体感してみましょう.
この分割が可能なことは,パンケーキの定理によって保証されています.仮に二つの図形A,B が共に長方形の形をしていれば,各々の中心(対角線の交点) を通る直線で一刀両断すれば良いことが分かります.ハムサンドウィッチ,パンケーキ,何だか親近感がわいてきました.少し背伸びをして,大学で学ぶ数学を垣間見ることにしましょう. |
| 年度 | 平成22年度 |
|---|---|
| 日付 | 平成22年8月5日(木) |
| 概要 |
『ギャンブルは儲かるか』 小池 健一 先生 競輪,競馬,競艇を始めとして,世の中には多くのギャンブルがあります. また,ジャンボ宝くじ,ロト,ナンバーズのような宝くじについても, 一獲千金を夢見て発売当日から売り場に並ぶ人たちがニュースによく登場します. これらは本当に儲かるのでしょうか? ギャンブルと確率論は密接な関係があります.そもそも確率論の始まりが, シュバリエ・ド・メレ(1607-1684)がブレイズ・パスカル(1623-1662)に以下のような問題を出し, それをパスカルがピエール・ド・フェルマー(1601-1665)と手紙をやりとりして考えたことである とされています.
起こりうる事象を全て列記し,そのうちのある事象が起こる回数を数え上げてその比率を求めれば, その事象の確からしさが求められます.このような考察から確率論は生まれました. 現実社会においては,結果があらかじめ分からないことが数多くあります. しかもそのようなことに我々の生活が依存しています.このリスクに対して, 我々はどのように立ち向かっていくべきでしょうか. それには,確率を用いてリスクを見積もるのがよいのです. 今回の体験学習では,ギャンブルに関する問題を確率や期待値の概念を使って様々な観点から考えてみることにしましょう. |
| 年度 | 平成21年度 |
|---|---|
| 日付 | 平成21年8月6日(木) |
| 概要 |
『微分方程式で、鑑定しよう!』 国宝級の絵画や工芸品が発見されたとき、如何にしてそれが本物か偽物かを 見抜くのでしょうか?実は、ある化学物質の変化に注目することで、加工され てから経った時間がわかり、本物か偽物かを鑑定できます。 日常生活でお茶が冷めて苦いと、ヤカンでお茶を製造(加工)してから時間が 経っていることが感覚的にわかるでしょう。短時間前ならば、温度差から次の 関係式(冷却に関するニュートンの法則)を用いて時間を求めることが可能です。 dF(t)/dt =kF(t) ここで、kは物質から決まる定数で、tは時間、Fは温度差と表す関数とします。 このような関係式を微分方程式と呼びます。長時間前ならば、お茶の苦み(酸化) の変化からも同じような微分方程式を用いて時間を求めることが可能です。 今回の体験学習では、“微分”という演算をわかりやすく説明し、微分方程式 の解き方を説明します。そして、美術品の制作(加工)時期を求める年代測定に 挑戦しましょう!具体的には、次のウィンチェスター城の壁に取り付けられて いる円卓を調べてみます。
※)微分方程式を用いて年代測定を行い、この円卓が“長時間前”である遠い昔 5世紀頃実際に実在したアーサー王の円卓であるかどうかを鑑定できます。 |
| 年度 | 平成20年度 |
|---|---|
| 日付 | 平成20年8月7日(木) |
| 概要 |
『(ミニ)ルービックキューブに挑戦!』 簡単そうに見えますが実はかなり難しいパズルで、やみくもにキューブを回していてもまず解けません。なにせ、ルービックキューブに回転操作を施すことで起こりうる色の配置パターンは、ナント、 43,252,003,274,489,856,000通り もありますから。 このようにとても難解なルービックキューブですが、その数学的な構造(もう少し詳しくいうと、群論的な構造)をじっくり調べることで解法が見えてきます。体験学習では、サイズがひと回り小さい2×2×2のミニルービックキューブを使って、 Q.ミニルービックキューブの色の配置のパターンは何通りあるか? という問題を考え、その数え上げの過程で見えてくるミニルービックキューブの解法について紹介したいと思います。難解なパズルを通して、群論や組合せ論の世界を覗いてみましょう! |
| 年度 | 平成19年度 |
|---|---|
| 日付 | 平成19年8月3日(金) |
| 概要 |
『連立方程式の応用―スプライン曲線と温度分布―』 スプライン曲線はコンピュータグラフィックスなどで利用されている曲線です。平面に順番を付けた点をプロットし、これらの点を順番通りに通っていく滑らかな曲線を描こうというのが、スプライン曲線の目的です。点を順番通りに通っていく滑らかな曲線ということが、この場合の望む条件になります。そして、そのような曲線を見つけようとすると、連立方程式が現れます。 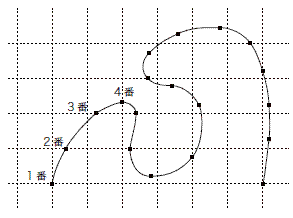 次は温度分布です。金属の板の一部に熱いものが触れているときに、その板の温度の分布はどうなっているでしょうか。温度は場所によって違いますし、時間によっても変化しますが、時間が経過すると同じ場所の温度は変化しなくなります。この場合、一点のまわりの温度の平均がその点の温度に一致します。金属の板の上に細かい格子を描いて、まわりの点の温度の平均がその点の温度になるということを板全体で考えると連立方程式になります。 どちらの場合も微分の考え方が基礎にあって連立方程式が導かれるのですが、なるべく直感に訴えるわかりやすい説明を心掛けます。  9:15~9:30 受付 1D201前 9:30~9:40 実行委員長(数学類長)挨拶及び事務連絡 1D201 9:40~9:50 講義の行われる教室(1E棟4階)に移動 9:50~11:50 講義と演習 11:50~13:00 昼休み 学生食堂などに案内します 13:00~15:00 講義と演習 15:00~16:30 放課後 在学生との懇談会 16:30~17:00 写真撮影 感想をひと言 |
| 年度 | 平成18年度 |
|---|---|
| 日付 | 平成18年8月4日(金) |
| 概要 |
『切ったり貼ったり ―― デーンの定理とその周辺 ――』  10:00 ~ 12:00 講義 切ったり貼ったり ― デーンの定理とその周辺 ―(坂井 公) 12:00 ~ 13:00 昼休み 学生食堂などに案内します 13:00 ~ 15:00 演習 坂井 公 先生と在学生 15:00 ~ 16:30 放課後 在学生との懇談会 16:30 終了証授与 写真撮影 感想 |
| 年度 | 平成17年度 |
|---|---|
| 日付 | 平成17年8月4日(木) |
| 概要 |
『p-進世界へようこそ』 この講義では、「実数」と平行して存在する「p-進数」と呼ばれる新たな数の世界をご案内します。新世界を訪れるときは誰もが感じるように、始めはこの「p-進世界」も奇妙な世界に見えるでしょうが、最後には p-進世界も(実数世界と同じく)豊かな面白い世界だということを体験していただきたいと思います。 『ギャンブルの数学』 では大学の確率論では何をするかと言えば、自然現象や経済等に現れる偶然現象を数学的に厳密に定式化して議論してみようということです。世の中には競馬競輪といったギャンブルに縁の無い人でも、何かの決断をするときに、運不運を考慮せざるを得ない場面は多いと思います。どこの大学を受験しようかとか、今日は傘を持って出るべきかとか。そのような場合、確率論は魔法のように正解を教えてくれるわけではありませんが、何が合理的かを教えてくれます。偶然がからむ場面では、運の良い者と合理的な者が得をし、 不運な者と不合理な者が損をします。運の方は仕方がありませんから、何が合理的かについて考えたいと思います。  10:00 ~ 12:00講義p-進世界へようこそ (山崎隆雄先生) 12:00 ~ 13:00昼休み学生食堂などに案内します 13:00 ~ 15:00講義ギャンブルの数学 (笠原勇二先生) 15:00 ~ 16:30放課後おやつ + 在学生との懇談会 16:30 終了証授与 写真撮影
|
| 年度 | 平成15年度 |
|---|---|
| 日付 | 平成15年8月8日(金) |
| 概要 |
『素数は数えられそうか』 『曲線の微分トポロジー』  9:15 ~ 9:30 受付 |
| 年度 | 平成11年度 |
|---|---|
| 日付 | 平成12年3月20日(月)~21日(火) |
| 概要 |
[代数] 『ベクトル空間のお話』
 平成12年3月20日(月) 3月21日(火) |
| 年度 | 平成10年度 |
|---|---|
| 日付 | 平成11年3月19日(金)~20日(土) |
| 概要 |
[代数] 『何通り?群を使えばこの通り』
 平成11年3月19日(金) 3月20日(土) |
| 年度 | 平成9年度 |
|---|---|
| 日付 | 平成10年3月19日(木)~20日(金) |
| 概要 |
[代数] 『分割数とその周辺』
 平成10年3月19日(木)
|
| 年度 | 平成8年度 |
|---|---|
| 日付 | 平成9年3月19日(水)~20日(木) |
| 概要 |
[代数] 『リー代数入門(微分とその仲間達)』 宮本雅彦
 平成9年3月19日(木) 3月20日(金) |
| 年度 | 平成7年度 |
|---|---|
| 日付 | 平成8年3月19日(火)~20日(水) |
| 概要 |
 平成8年3月19日(火)
|
| 年度 | 平成6年度 |
|---|---|
| 日付 | 平成7年3月20日(月)~21日(火) |
| 概要 |
平成7年3月20日(月)
14:40--16:00 まとめ |
| 年度 | 平成5年度 |
|---|---|
| 日付 | 平成6年3月21日(月)~22日(火) |
| 概要 |
平成6年3月21日(月)
|
| 年度 | 平成24年度 |
|---|---|
| 日付 | 平成24年8月2日 |
| 概要 |
『面積を数えよう』 竹山 美宏 先生  私たちは, 小学校の算数で長方形や三角形, 平行四辺形などの面積の公式を学びました. どの公式も, 辺の長さや高さを足したり掛けたり2で割ったりするものですから, 面積を計算するためには(長さを)『測る』という操作が必要なはずです. ところが, ある世界では面積を『数えて』計算することができます. 私たちは, 小学校の算数で長方形や三角形, 平行四辺形などの面積の公式を学びました. どの公式も, 辺の長さや高さを足したり掛けたり2で割ったりするものですから, 面積を計算するためには(長さを)『測る』という操作が必要なはずです. ところが, ある世界では面積を『数えて』計算することができます.舞台となるのは下の図のように点が等間隔に並んだ世界です. この点を頂点とする多角形を考えます. 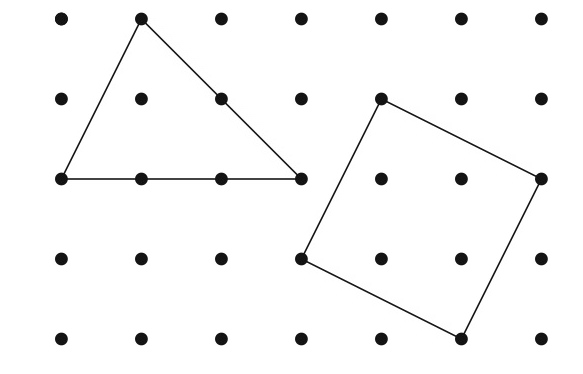 点の間隔を1としましょう. すると, 左の三角形の底辺の長さは3, 高さは2ですから, 面積は 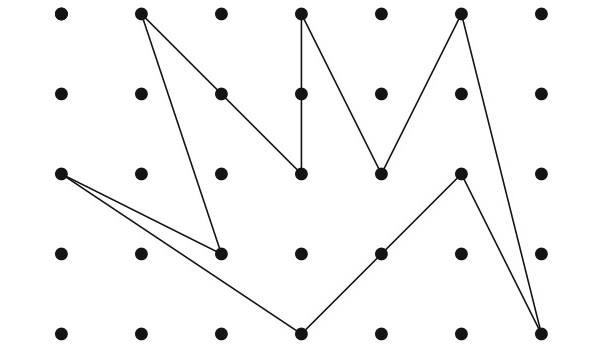 このように複雑な場合は, 普通に面積を計算すると大変です. 実は, 上の多角形の面積は次の式で求められます. この計算では, あるものを『数えて』面積を求めているのですが・・・. 今回の体験学習では, 上の問題を通じて, 参加者のみなさんと一緒に数学の研究を疑似体験してみようと思います.        |











































 『多変数関数の微分と積分』
『多変数関数の微分と積分』 『曲がった空間―曲率は全てを語る』
『曲がった空間―曲率は全てを語る』

 『民主主義国家構築のために』
『民主主義国家構築のために』
 平成14年7月27日(土)
平成14年7月27日(土) 7月28日(日)
7月28日(日)