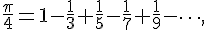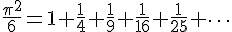過去の体験学習
年度
平成13年度
日付
平成13年7月28日(土)~29日(日)
概要
[代数] 『定規とコンパスによる作図』
[幾何] 『楽しい結び目・絡み目の数学』
[解析] 『応用数学における微分方程式入門』 現代、応用する立場の人々から見た数学を捉えてみましょう。その1例として、ここでは微分方程式を取り上げますが、予備知識としては、簡単な多項式の微分がわかれば十分です。そのなかでも、指数関数の別の定義の仕方を導出することによって、指数関数の性質を別な方法で導き出すことができます。この別な方法は、高校で習う方法よりも、ときとしてスッキリした形で表わされることがありますので、そのいくつかを見てみましょう。また、今までは数の指数関数、つまり、1次元ベクトル(スカラー)の指数関数を見て来ました。現代数学では、この概念を拡張して、n次元ベクトルの指数関数や無限次元の指数関数さらに非線形の指数関数が定義されます。こうした新しい数学が、間接的に天気予報や航空機の設計に役立っております。
[情報] 『いくつかのものを統計的に比較してみよう』
平成13年7月28日(土)講義 『定規とコンパスによる作図』 藤田 尚昌講義 『楽しい結び目・絡み目の数学』 金戸 武司
7月29日(日)講義 『応用数学における微分方程式入門』 山崎 満講義 『いくつかのものを統計的に比較してみよう』 青嶋 誠
年度
平成12年度
日付
平成13年3月19日(月)~20日(火)
概要
[代数] 『円周率を巡る御伽噺』
[幾何] 『曲線の幾何学』
[解析] 『「つむじ」の数を数えてみよう』
[情報] 『切ったり貼ったり-デーンの定理とその周辺-』
平成13年3月19日(月)講義 『円周率を巡る御伽噺』 増田 哲也講義 『曲線の幾何学』 長友 康行
3月20日(火)講義 『「つむじ」の数を数えてみよう』 竹内 潔講義 「切ったり貼ったり-デーンの定理とその周辺-」 坂井 公
年度
平成11年度
日付
平成12年3月20日(月)~21日(火)
概要
[代数] 『ベクトル空間のお話』
平成12年3月20日(月)講義 『結び目理論入門』 川村 一宏講義 『ベクトル空間のお話』 加藤 豊紀講義 『数学的帰納法の原理』 本橋 信義
3月21日(火)講義 『微分方程式とケプラーの法則』 土居 伸一
年度
平成10年度
日付
平成11年3月19日(金)~20日(土)
概要
[代数] 『何通り?群を使えばこの通り』
平成11年3月19日(金)講義 『何通り?群を使えばこの通り』増岡 彰講義 『双曲幾何へのいざない』伊藤光弘講義 『統計学は未来を予測できるか?』赤平昌文
3月20日(土)講義 『フーリエ級数と無限級数』筧 知之
年度
平成9年度
日付
平成10年3月19日(木)~20日(金)
概要
[代数] 『分割数とその周辺』
平成10年3月19日(木)講義 『分割数とその周辺』内藤 聡講義 『トポロジーの世界』酒井克郎
講義 『微積分学入門』南 就将講義 『鶴亀算のかなた(グレブナー基底理論入門)』坂井 公
年度
平成8年度
日付
平成9年3月19日(水)~20日(木)
概要
[代数] 『リー代数入門(微分とその仲間達)』
平成9年3月19日(木)
3月20日(金)
年度
平成7年度
日付
平成8年3月19日(火)~20日(水)
概要
平成8年3月19日(火)
年度
平成6年度
日付
平成7年3月20日(月)~21日(火)
概要
平成7年3月20日(月)講義 『方程式の解法と群(代数学入門)』森田 純講義 『曲面とその曲率』伊藤光弘
講義 『円周率πの計算』若林誠一郎講義 『コンピュータは因数分解をどう行うのか?』佐々木建昭
14:40--16:00 まとめ
年度
平成5年度
日付
平成6年3月21日(月)~22日(火)
概要
平成6年3月21日(月)講義 『方程式とガロアの理論』木村達雄講義 『作用素の指数関数』村松壽延
講義 『集合論帝国主義』本橋信義講義 『微積分と等周問題』高橋恒郎
年度
平成24年度
日付
平成24年8月2日
概要
『面積を数えよう』 私たちは, 小学校の算数で長方形や三角形, 平行四辺形などの面積の公式を学びました. どの公式も, 辺の長さや高さを足したり掛けたり2で割ったりするものですから, 面積を計算するためには(長さを)『測る』という操作が必要なはずです. ところが, ある世界では面積を『数えて』計算することができます.
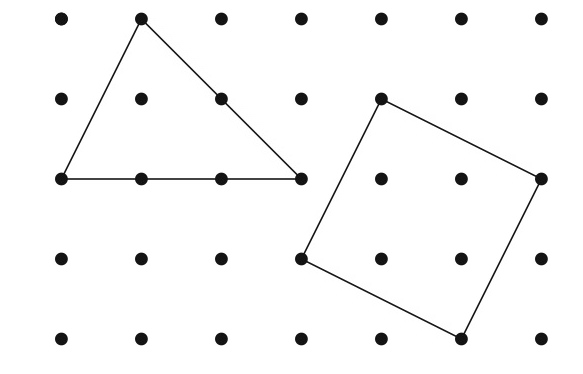
舞台となるのは下の図のように点が等間隔に並んだ世界です. この点を頂点とする多角形を考えます.
点の間隔を1としましょう. すると, 左の三角形の底辺の長さは3, 高さは2ですから, 面積は
です. 右の四角形は正方形で, 一辺の長さは
$$\sqrt{5}$$ ですから, 面積は
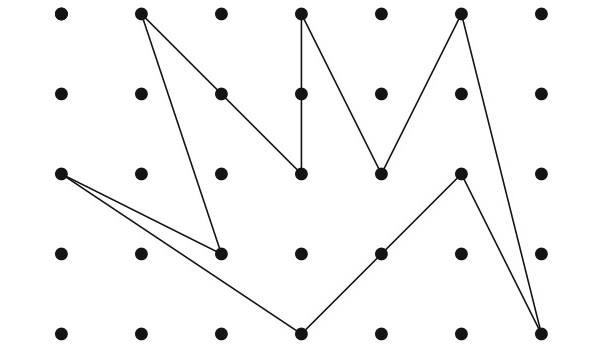
$$\sqrt{5} \times \sqrt{5}=5$$ です. では, 下の多角形の面積はいくつでしょうか?
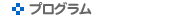

 私たちは, 小学校の算数で長方形や三角形, 平行四辺形などの面積の公式を学びました. どの公式も, 辺の長さや高さを足したり掛けたり2で割ったりするものですから, 面積を計算するためには(長さを)『測る』という操作が必要なはずです. ところが, ある世界では面積を『数えて』計算することができます.
私たちは, 小学校の算数で長方形や三角形, 平行四辺形などの面積の公式を学びました. どの公式も, 辺の長さや高さを足したり掛けたり2で割ったりするものですから, 面積を計算するためには(長さを)『測る』という操作が必要なはずです. ところが, ある世界では面積を『数えて』計算することができます.