 数学者のイメージ
数学者のイメージ
数学者の変人ぶり、奇行の話は面白いし大衆受けするので孤高、狂気と紙一重、という文章や映像受けするイメージが作られていますが、好きではありません。本当は、「素朴で、何か少しこだわりが強く馬鹿正直で嘘がつけない人たち」というのが平均的なのではないかなあ。
 研究の内容は
研究の内容は
数論とエルゴード理論の境界領域です。
数論とエルゴード理論
どちらも歴史が長く大変広い分野です。数学の問題の多くにはアナログとデジタル、連続と離散の違いがあります。離散的な問いは多くの場合、記述は易しいけれど問題自体はとても難しくなります。離散で難しい問題ならいくらでも挙げることができますが、解ける問題は少ないしヒントも手掛かりもない。そのような問題に少しでも手がつけば数論の研究者は「面白い」と感じます。一方でエルゴード理論は、もともと統計力学の発展の中で生まれ、閉じた系での粒子の軌道の平均的で大雑把な性質を調べる学問です。この理論で大事なのは一種の「予定調和」で、落とし所はある程度直感的に見えるけれど、それをどのように厳密にするかが分からない事が多い。そういう感じがする学問です。
研究者気質
個人的な印象ですが、数論は技術を極める職人の世界、エルゴード理論は細かいことを気にしない芸術家肌の世界です。(数学で「細かいことを気にしない」というのはもちろん程度の問題で他分野からすれば形容矛盾かも。)その研究の内容の差が、実際の研究での思考法の差にも現れているように思います。数論研究者の多くが、繊細で細部を非常に重視します。針に糸を通すようなしかも長い背理法を用いたりするので高い緊張を要します。エルゴード理論では、問題の全体をどのように見ているかというような、幾何学的で大局的なものの見方が問われます。研究者は雑駁で気さく。話し合って進んだりするのも好きな人が多いようです。
 準自己相似タイル張りの例
準自己相似タイル張りの例
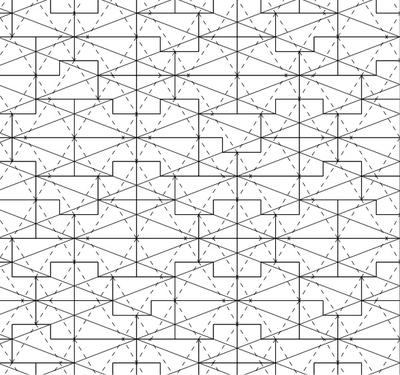 Ammannによる強非周期的タイル張り
Ammannによる強非周期的タイル張り
タイル張り力学系
私が最近面白いと思っているのはタイル張りの力学系というものです。タイル張りの分類自体は非常に古くからある問題ですが、その力学系を考えるのは比較的最近の流れです。数論のアルゴリズムと関連して自然に現れ比較的カオス的でない硬い力学系になります。このような力学系は、代数、幾何、解析、情報数学などの様々な道具で調べることができ、いろいろな数学を応用できます。2011年にシェヒトマンが準結晶の発見でノーベル化学賞を受賞しましたが、タイル張り力学系はその構造のモデルを与えることが一つの研究の目的です。
 上記の準自己相似タイルを自己相似性を持つものに変換した像
上記の準自己相似タイルを自己相似性を持つものに変換した像
 自分は数学に向いているかどうか
自分は数学に向いているかどうか
こういう質問をよく受けます。私には答える資格があるかわかりません。いまだに自分自身が本当に向いているかもよくわからない。一つだけはっきり言えることがあります。自分が数学に向いているかどうかを、あまり真面目に気にする人は数学には向いていないということです。数学は勉強すると楽しいし問題をかんがえていると時間を忘れてしまう。自分の将来というような問題を考えるより、難しい問題を黙って考えるほうが楽しい。そんな人に向いている学問と思います。

 開かれた数学
開かれた数学
一方で数学を目指す人には、分野にかかわらず様々な数学、物理、化学、生物、地学などの自然科学一般、さらに文学や社会科学にも好奇心と興味を持ってほしいと思っています。そうすることで将来本当に数学が楽しめるからです。数学は、本質的に自然科学、社会科学の基本言語で、様々な外部からの刺激を素材に形を変えています。形を変え変化していく事は数学の宿命で、また、いかなる形にもなりうる事が面白いのです。様々な分野の境界にある数学が生き生きと発展していくように感じます。













